MOVIMIENTO CIRCULAR EN EL UNIVERSO Y EN EL ÁTOMO
1. Relación angular y lineal
Relación entre las magnitudes angulares y lineales
Magnitudes lineales y angulares
De la definición de radián (unidad natural de medida de ángulos) obtenemos la relación entre el arco y el radio. Como vemos en la figura, el ángulo se obtiene dividiendo la longitud del arco entre su radio
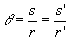
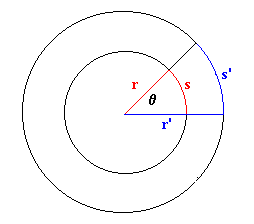
Derivando s=rq respecto del tiempo obtenemos la relación entre la velocidad lineal y la velocidad angular
La dirección de la velocidad es tangente a la trayectoria circular, es decir, perpendicular a la dirección radial
Derivando esta última relación con respecto del tiempo obtenemos la relación entre la aceleración tangencial at y la aceleración angular.
Existe aceleración tangencial, siempre que el módulo de la velocidad cambie con el tiempo, es decir, en un movimiento circular no uniforme.
El cálculo de la componente normal de la aceleración es algo más complicado. La aceleración normal está relacionada con el cambio de la dirección de la velocidad con el tiempo. En un movimiento circular uniforme no existe aceleración tangencial ya que le módulo de la velocidad no cambia con el tiempo, solamente cambia su dirección y por tanto, solamente existe aceleración normal.
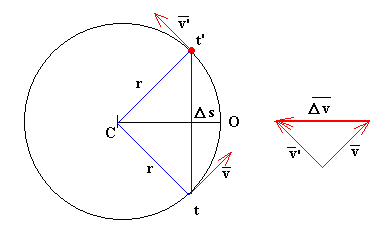
Supongamos
un móvil que describe un movimiento circular uniforme. Calculemos el cambio de
velocidad
que
experimenta el móvil entre los instantes t y t', tal como se ve
en la figura. El vector
tiene dirección radial y sentido hacia el centro
de la circunferencia. Los triángulos de color rojo y de color azul de la figura son
isósceles semejantes por lo que podemos establecer la siguiente relación
Dividiendo ambos miembros entre el intervalo de tiempo Dt=t'-t
Cuando el intervalo de tiempo Dt tiende a cero, la cuerda Ds se aproxima al arco, y el cociente ds/dt nos da la velocidad v del móvil
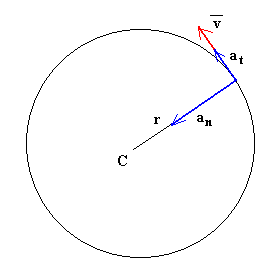
La aceleración normal an tiene dirección radial y sentido hacia el centro de la circunferencia que describe el móvil y su módulo viene dado por una u otra de las expresiones siguientes:
La velocidad de un móvil en movimiento circular tiene la dirección tangente a la circunferencia.
Existe aceleración tangencial at siempre que cambie el módulo de la velocidad con el tiempo. El sentido de la aceleración tangencial es el mismo que el de la velocidad si el móvil acelera, y es de sentido contrario si se frena. En un movimiento circular uniforme no hay aceleración tangencial.
En un movimiento circular siempre existe aceleración normal, an ya que cambia la dirección de la velocidad con el tiempo. La aceleración normal tiene dirección radial y sentido hacia el centro de la circunferencia que describe el móvil.
La aceleración total del móvil se obtiene sumando vectorialmente ambas componentes de la aceleración
Ver más en el video