MANIFESTACIONES GRAVITACIONALES DE LA MADRE TIERRA Y EL COSMOS
3. Movimientos relativos y dependientes
Movimiento relativo y movimiento dependiente
Cuando varias partículas se mueven independientemente a lo largo de la misma línea pueden escribirse ecuaciones de movimiento
independiente para cada partícula Siempre que sea posible, el tiempo debe registrarse desde el mismo instante inicial para todas las partículas y los desplazamientos deben medirse a partir del mismo punto de referencia y en la misma dirección.Movimiento relativo.- Imagina dos partículas A y B moviéndose a lo largo de la misma recta como lo muestra la siguiente figura:
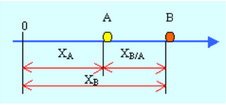
Movimientos Dependientes. Algunas veces, la posición de una partícula dependerá de la posición de otra o de varias partículas. En este caso se dice que los movimientos son dependientes. Por ejemplo, la posición del bloque B en la figura depende de la posición del bloque A. Puesto que la cuerda ACDEFG es de longitud constante y puesto que las longitudes de las porciones de cuerda CD y EF alrededor de las poleas permanecen constantes, se concluye que la suma de las longitudes de los segmentos AC, DE y FG es constante. Al observar que la longitud del segmento AC difiere de xA sólo por una constante y que de manera similar, las longitudes de los segmentos DE y FG difieren de xB únicamente por una constante, se escribe:
Puesto que sólo una de las dos coordenadas xA y xB pueden elegirse de manera arbitraria, se afirma que el sistema que se presenta un grado de libertad, por ejemplo en la siguiente gráfica observe:
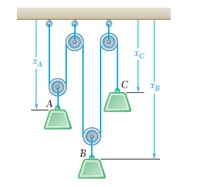
Existen tres coordenadas xA , xB y xC y el sistema presenta dos grados de libertad.
cuando la relación que existe entre las coordenadas de posición de varias partículas es lineal, se cumple una relación similar entre las velocidades y aceleraciones de las partículas. En el caso de los bloques de la figura anterior, se diferencia dos veces la ecuación obtenida y se escribe:
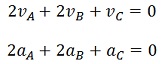
Más sobre movimientos dependientes