PROGRESIONES Y ANÁLISIS COMBINATORIO APLICADOS EN DIFERENTES CONTEXTOS

6.1. Número combinatorio

Números combinatorios

Las agrupaciones combinatorias que sólo consideran la esencia de los grupos formados y no su orden, llamadas combinaciones, han constituido una rama específica dentro de la especialidad del análisis combinatorio, con múltiples usos en diversos campos. La expresión numérica de tales combinaciones recibe el nombre de número combinatorio o coeficiente binómico.

Coeficientes binómicos

Se define número combinatorio o coeficiente binómico como el valor numérico de las combinaciones ordinarias (sin repetición) de un conjunto de n elementos tomados en grupos de r, siendo n y r dos números enteros y positivos tales que n ³ r. Matemáticamente, un número combinatorio se expresa como:

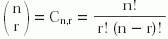
Propiedades de los números combinatorios

Los números combinatorios presentan algunas propiedades muy interesantes que justifican el amplio uso que se hace de ellos en algunas ramas científicas:

• Primera propiedad de los números combinatorios:

• Segunda propiedad de los números combinatorios.

Otras propiedades generales de los números combinatorios son las siguientes:

• Cualquier número sobre 0 es igual a 1.
• Todo número sobre sí mismo es igual a 1.
• Un número sobre 1 es siempre igual al número.