LOGARITMOS Y EXPONENTES EN LA REALIDAD COTIDIANA

1. Definición y cálculo de un logaritmo

1.1. Propiedades logarítmicas

Logaritmos y sus propiedades

1- Definición de Logaritmo

Se define logaritmo como el exponente de una potencia con cierta base, es decir, el número al cual se debe elevar una base dada para obtener un resultado determinado.

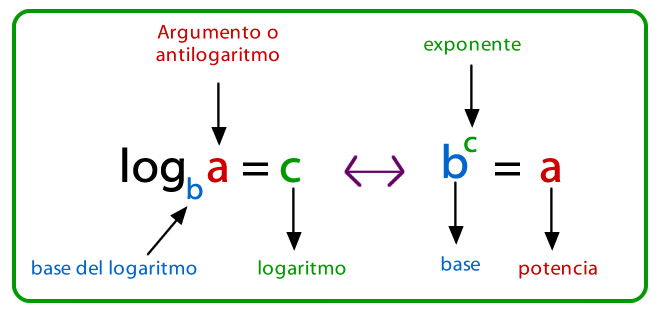
Por ejemplo:

5 ⁰ = 1

5¹ = 5

5² = 25

5³ = 125, etc.

Luego, siendo la base 5, el logaritmo de 1 (que se escribe log₅ 1) es 0, por que 0 es el exponente al que hay que elevar la base 5 para que dé 1; el log₅ 5 es 1; el log₅ 25 es 2, el log₅ 125 es 3, etc.

- No existe el logaritmo de los números negativos.

El argumento y la base de un logaritmo son números reales positivos. Además, la base no puede ser 1. Es decir, en la expresión log_b a, siempre, por definición, a ∈ R⁺ y b ∈ R⁺ – {1}.

- La expresión log_b a , se lee como: “logaritmo de a en base b”.

Volvamos a la definición de logaritmo: “exponente al que es necesario elevar una cantidad positiva para que resulte un número determinado”.Si lo escribiera como ecuación, corresponde a resolver log_b a = x, donde b es la base del logaritmo y a es su argumento, con a y b positivos.

- El argumento y la base de un logaritmo son números reales positivos. Además, la base no puede ser 1. Es decir, en la expresión log_b a, siempre, por definición, a ∈ R⁺ y b ∈ R⁺ – {1}.

- La expresión log_b a , se lee como: “logaritmo de a en base b”.

Volvamos a la definición de logaritmo: “exponente al que es necesario elevar una cantidad positiva para que resulte un número determinado”.Si lo escribiera como ecuación, corresponde a resolver log_b a = x, donde b es la base del logaritmo y a es su argumento, con a y b positivos.

Ejemplo1:

- Calcula el valor de log₇ 343

equivale a resolver la ecuación:

log₇ 343 = x

Entonces, ya que la base del logaritmo es 7, el exponente no se conoce y 343 es el argumento, es decir, el valor de la potencia, se puede escribir:

7^x =343

7^x = 7³

luego, igualando los exponentes, se concluye que

x= 3

Ejemplo 2:

- Calcula el valor de log_0,7 0,343

equivale a resolver la ecuación:

log_0,7 0,343 = x

Luego:

0,7^x = 0,343

0,7^x = (0,7)³

Luego, igualando exponentes tenemos:

x=3

log_0,7 0,343 = 3

Para una definición más completa de logaritmos, se determinarán restricciones respecto de su base y su argumento.

2- Propiedades

2.1- Logaritmo de la unidad

El logaritmo de 1 en cualquier base es igual a 0.

log_b (1) = 0 ; con b ≠ 1.

Ej: log₅ (1) = 0 porque 5⁰ =1

log₇(1) = 0 porque 7⁰ = 1

log₂₀ 1 = 0 ⇔ 20⁰= 1

2.2- Logaritmos de la base

El logaritmo de la base es igual a 1.

log_b (b) = 1 ; con b ≠ 1.

Ej:

log₅ (5) = 1 ⇔ 5¹ = 5

log₆ (6) = 1 ⇔ 6¹ = 6

log₁₂ (12) = 1 ⇔ 12¹ = 12

2.3- Logaritmo de una potencia con igual base:

El logaritmo de una potencia de un número es igual al producto entre el exponente de la potencia y el logaritmo del número.

log_b bⁿ = n, con b ≠ 1

Ej:

log₆ 6 ³ = 3

2.4- Logaritmo de un producto

El logaritmo de un producto es igual a la suma de los logaritmos de los factores.

log_b (a • c) = log_b a + log_b c

Ej:

log_b (5 • 2) = log_b 5 + log_b 2
2.5- Logaritmos de un cociente
El logaritmo de un cociente es igual al logaritmo del dividendo, menos el logaritmo del divisor.

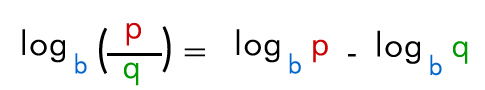
Ej:

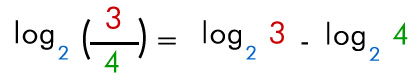
2.6- Logaritmo de una potencia

El logaritmo de una potencia es igual al exponente multiplicado por el logaritmo de la base.

log_a cⁿ = n log_a c
Ej:

log₃ 10 ² = 2 log₃ 10
2.7- Logaritmo de una raíz

El logaritmo de una raíz es igual al logaritmo de la cantidad subradical dividido entre el índice de la raíz.

Ej:

2.8- Cambio de base

para todo p, a, b > 0; b, c ≠ 1

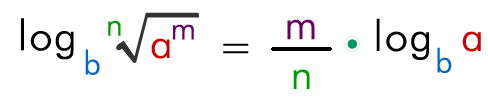
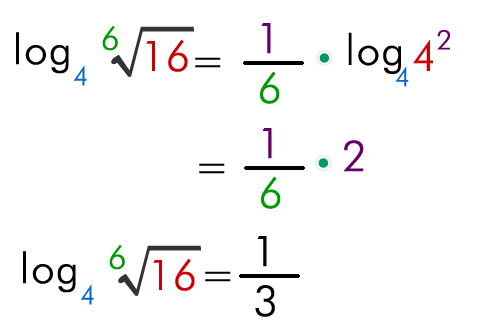
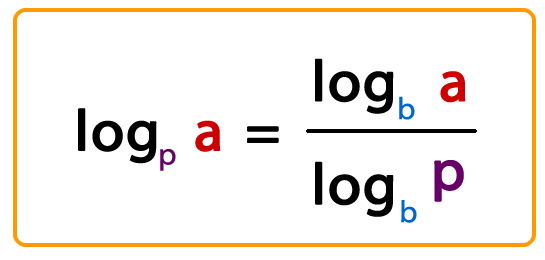
Ej:

log₂ 5 = log 5 / log 2

Más información de propiedades de los logaritmos