INECUACIONES Y NÚMEROS COMPLEJOS
1. Desigualdades e inecuaciones
1.1. Inecuaciones de primer y segundo grado
Sistemas de inecuaciones con una incógnita de primer y segundo grado
A continuación te voy a explicar cómo resolver sistemas de inecuaciones lineales o de primer grado con una incógnita, así como sistemas de inecuaciones de segundo grado con una incógnita.
Lo veremos con ejercicios resueltos paso a paso.
¡Empezamos!
Solución de un sistema de ecuaciones con una incógnita
Tal y como explico en el Curso de Inecuaciones, una inecuación con una incógnita tiene como solución un rango de valores.
Pues bien.
En un sistema de inecuaciones con una incógnita, la solución estará formada por el rango de valores en el cual se solapen cada una de las soluciones de las inecuaciones que forman el sistema.
Cualquier valor que se encuentre dentro de ese intervalo cumplirá las desigualdades de todas las inecuaciones.
Si no hay ningún rango de valores donde se solapen todas las soluciones, el sistema no tendría solución.
Lo verás más claro cuando vayamos resolviendo ejercicios.
Para poder resolver un sistema de inecuaciones de primer y segundo grado con una incógnita, es necesario que sepas resolver por separado inecuaciones de primer grado como inecuaciones segundo grado.
Vamos a empezar por resolver sistemas de ecuaciones de primer grado con una incógnita.
Cómo resolver sistemas de ecuaciones lineales de primer grado con una incógnita
Los sistemas de inecuaciones lineales de primer grado con una incógnita
son aquellos donde todas las inecuaciones que forman el sistema son inecuaciones de primer grado, como por ejemplo:
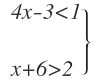
Para resolver este sistema, tenemos que resolver por separado cada inecuación y después, el rango de valores donde coincidan ambas soluciones será la solución del sistema.
Empezamos resolviendo la primera inecuación:
![]()
Operamos en el segundo miembro:
![]()
Y pasamos el 4 dividiendo al segundo miembro:
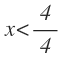
Volvemos a operar y llegamos a su solución:
![]()
Los valores de x que sean menores que 1, o el intervalo (-∞,1), que si lo representamos en al recta, queda de la siguiente mantera:
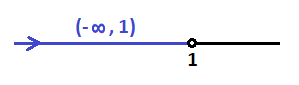
Seguimos resolviendo la segunda inecuación:
![]()
Y operamos:
![]()

Una vez tenemos ambas soluciones por separado, representamos ambas
soluciones juntas en la recta. El intervalo donde se solapen ambas
soluciones será la solución del sistema:

En nuestro caso es el intervalo (-4,1):
Cómo resolver sistemas de ecuaciones de segundo grado con una incógnita
Los sistemas de inecuaciones de segundo grado con una incógnita son aquellos donde al menos una de las inecuaciones que forman el sistema es una inecuación de segundo grado.
Por ejemplo:
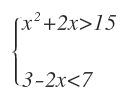
Vamos a ver cómo resolver este sistema. El procedimiento es el mismo que en el caso anterior, solo que ahora tenemos una inecuación de segundo grado y por tanto, se resuelve de una forma distinta a las de primer grado.
Empezamos resolviendo la primera inecuación, que se trata de una inecuación de segundo grado:
![]()
Pasamos el 15 al primer miembro:
![]()
Y resolvemos la ecuación de segundo grado que resulta al cambiar la desigualdad por el signo igual:
![]()
Cuyas soluciones son:
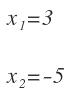
Las representamos en la recta real:

Y ahora tenemos que saber en qué tramos se cumple que es mayor que cero.
Le doy un valor a la x entre el -3 y 5 y veo que el resultado es negativo:
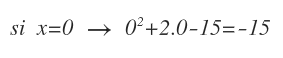
Luego en los otros 2 tramos será positivo:
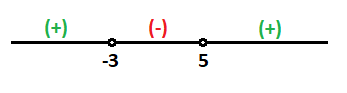
Por tanto, la solución de la inecuación de segundo grado es:
![]()
Es decir, los valores de x que sean menores que -3 y mayores que 5.
Ahora vamos a resolver la segunda inecuación:
![]()
En este caso es una inecuación de primer grado.
Pasamos el -2 dividiendo al segundo miembro y como es negativo, la damos la vuelta a la desigualdad:
![]()
Y finalmente nos queda:
![]()
La solución son los valores de x mayores que -2 o los que pertenecen al intervalo (-2,∞).
Representado en la recta real es:

Ya tenemos la solución de cada inecuación por separado.
Ahora tenemos que encontrar el rango de valores donde se solapen las dos soluciones.
Para ello, en la recta, dibujamos las dos soluciones, una encima de la otra:
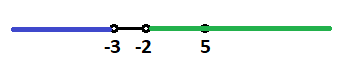
El tramo donde se solapan la línea azul (solución de la primera inecuación) y la línea verde (solución de la segunda inecuación) es el tramo rojo:

Por lo que la solución del sistema es desde 5 hasta infinito, sin coger
el 5, ya que es solución de la primera inecuación pero de la segunda no:
Cualquier valor que se sea mayor que 5 cumplirá las dos desigualdades del sistema.
Más sobre inecuaciones de Primer Grado
Inecuaciones de Segundo Grado (Cuadráticas)