INECUACIONES Y NÚMEROS COMPLEJOS

1.4. Sistemas de inecuaciones de primer y segundo grado

Inecuaciones y sistemas de inecuaciones de primer grado

Una inecuación es como una ecuación, con la diferencia de que cada uno de los dos miembros que la componen no está separado por el signo =

Sino por una desigualdad. Las desigualdades son cuatro: mayor >, menor <, mayor o igual ≥ y menor o igual ≤

No vamos a entrar aquí en un estudio exhaustivo de las propiedades de las desigualdades ni de las relaciones de orden en el conjunto de los números reales. Solamente destacaremos que las desigualdades se comportan como las igualdades para la operación suma pero de manera algo distinta para la operación producto.

Si sumamos (o restamos) la misma cantidad en los dos miembros de una desigualdad, la desigualdad no varía. En el caso de una inecuación obtenemos una inecuación equivalente. Igual ocurre con el producto si multiplicamos (o dividimos) los dos miembros de una desigualdad por la misma cantidad positiva: la desigualdad no varía. Sin embargo, si multiplicamos (o dividimos) los dos miembros de una inecuación por una misma cantidad negativa, la desigualdad cambia de sentido. Así pues, cuando manipulemos inecuaciones y multipliquemos o dividamos ambos miembros por la misma cantidad obtendremos inecuaciones equivalentes, pero tendremos cuidado cuando lo hagamos con una cantidad negativa pues en ese caso la inecuación equivalente a la anterior tendrá cambiado el sentido de la desigualdad. Mejor lo vemos con un ejemplo.

Resolvamos la siguiente inecuación de primer grado:

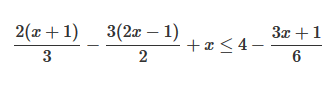
Se procede exactamente igual que en una ecuación de primer grado (eliminamos paréntesis y denominadores, trasponemos términos y reducimos términos semejantes). En este caso multiplicamos todos los términos (los dos miembros de la desigualdad) por 6, que es el mínimo común múltiplo de los denominadores y luego procedemos a ir simplificando hasta obtener una desigualdad completamente reducida.Veámoslo:

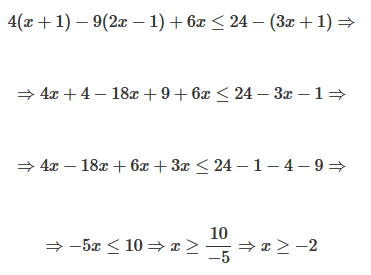
Obsérvese que, en el penúltimo paso, al dividir los dos miembros de la desigualdad entre −5, la desigualdad cambia de sentido. La solución de la inecuación, x≥−2, se puede escribir en forma de intervalo. En este caso la solución se corresponde con todos los números reales mayores o iguales que −2, es decir, el intervalo de números reales [−2, +∞). Obsérvese que este intervalo es cerrado por la izquierda (se denota con un corchete) pues la desigualdad, al tener el igual (no estricta), incluye al número −2

Para la representación gráfica de la solución trazamos, sobre la recta real, una flecha comenzando en −2
con sentido hacia la derecha, para significar que estamos tomando todos los números reales mayores que −2. Como se ha de incluir el extremo, el “circulito” que hace de origen de la flecha, lo “rellenamos”. De esta forma cerramos el intervalo incluyendo el extremo (en este caso −2).

Si lo que tenemos que resolver es un sistema lineal de dos o más inecuaciones con una incógnita, el procedimiento a seguir es resolver cada una de las inecuaciones por separado. Una vez hecho esto se representa gráficamente la solución de cada una de ellas. La parte simultánemente común de cada una de las soluciones es la solución del sistema. Si no hay parte común el sistema de inecuaciones no tiene solución. Veamos un ejemplo.

Resolveremos el siguiente sistema de inecuaciones:

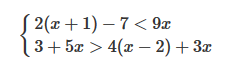
Para ello resolvemos en primer lugar la primera inecuación:

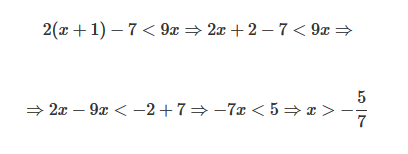
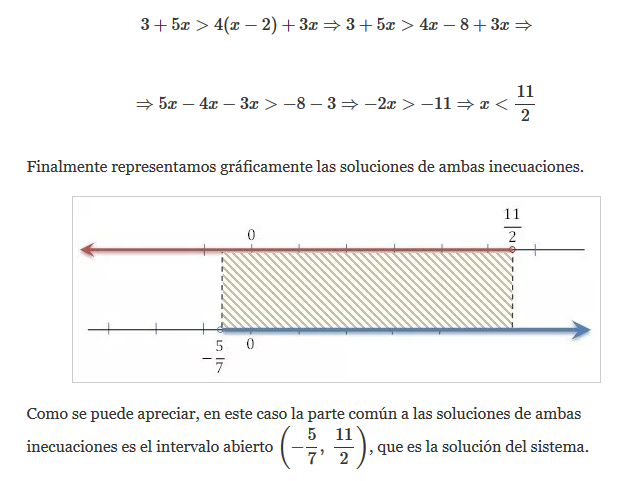
A continuación resolvemos la segunda inecuación:

Ver más sobre sistemas de inecuaciones de segundo grado