FUNCIONES Y ECUACIONES EN LA PRODUCTIVIDAD.

1.3. Gráfica de Sistema de Ecuaciones en el plano cartesiano.

Graficando sistemas de ecuaciones lineales

Recuerda que una ecuación lineal se grafica como una recta, que indica que todos los puntos de una recta son soluciones de la ecuación lineal. Existe un número infinito de soluciones. Si tenemos un sistema de ecuaciones lineales, la solución del sistema es el valor que hace válidas todas las ecuaciones. Para dos variables y dos ecuaciones, este es el punto donde las gráficas se intersectan. Las coordenadas de este punto serán la solución para las dos variables en las dos ecuaciones.

Sistemas de Ecuaciones

La solución de un sistema de ecuaciones es el valor o valores que hacen válidas a todas las ecuaciones en el sistema. Las gráficas de las ecuaciones del sistema te dicen cuántas soluciones existen para ese sistema. Observa las imágenes siguientes. Cada una muestra dos rectas que forman el sistema de ecuaciones.

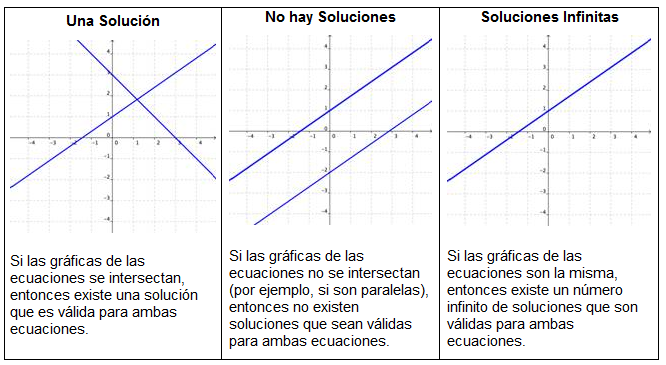
Cuando las rectas se intersectan, el punto de intersección es el único punto que las dos gráficas tienen en común, Entonces las coordenadas de ese punto son la solución de las dos variables usadas en las ecuaciones. Cuando las rectas son paralelas, no hay soluciones y a veces las dos ecuaciones se grafican como la misma recta, en tal caso tenemos un número infinito de soluciones.

Algunos términos especiales son usados a veces para describir tipos de sistemas.

Los siguientes términos se refieren a cuántas soluciones tiene el sistema.

•  Cuando un sistema tiene una solución (las gráficas de las ecuaciones se intersectan), es un sistema consistente de ecuaciones lineales y las ecuaciones son independientes.

•  Cuando el sistema no tiene solución (las gráficas de las ecuaciones no se intersectan), es un sistema inconsistente de ecuaciones lineales y las ecuaciones son independientes.

•  Si las rectas son la misma (las gráficas se intersectan en todos los puntos), es un sistema consistente de ecuaciones lineales y las ecuaciones son dependientes. Esto es, cualquier solución de una ecuación debe ser también una solución de la otra, por lo que las ecuaciones dependen una de la otra.

Los siguientes términos se refieren a si un sistema tiene soluciones.

•   El sistema es un sistema consistente de ecuaciones lineales cuando tiene soluciones.

•   El sistema es un sistema inconsistente de ecuaciones lineales cuando no tiene soluciones.