LA FORMA EN LA TECNOLOGÍA PROPIA Y APROPIADA

1. Geometría de nuestros pueblos y la geometría euclidiana:

Geometría Euclidiana

La geometría euclidiana corresponde al estudio de las propiedades de los espacios geométricos donde se satisfacen los axiomas de Euclides. Si bien este término a veces es usado para abarcar geometrías que tienen dimensiones superiores con propiedades parecidas, por lo general es sinónimo de geometría clásica o de geometría plana.

En el siglo III a. C. Euclides y sus discípulos escribieron los Elementos, una obra que englobaba el saber matemático de la época dotada de una estructura lógica-deductiva. Desde entonces la geometría se volvió una ciencia, inicialmente para resolver problemas clásicos y evolucionó hasta ser una ciencia formativa que ayuda a razonar.

Historia

Para hablar de la historia de la geometría euclidiana es imprescindible comenzar con Euclides de Alejandría y los Elementos.

Al quedar Egipto en manos de Ptolomeo I, después de la muerte de Alejandro Magno, este comenzó su proyecto en una escuela de Alejandría.

Entre los sabios que enseñaban en la escuela se encontraba Euclides. Se especula que su nacimiento data aproximadamente del 325 a. C. y su muerte del 265 a. C. Podemos saber con certeza que fue a la escuela de Platón.

Durante más de treinta años Euclides enseñó en Alejandría, construyendo sus famosos elementos: comenzó a escribir una descripción exhaustiva de las matemáticas de su tiempo. Las enseñanzas de Euclides produjeron excelentes discípulos, como Arquímedes y Apolonio de Perga.

Euclides se encargó de estructurar los descubrimientos dispares de los griegos clásicos en los Elementos, pero a diferencia de sus predecesores no se limita a afirmar que un teorema es verdadero; Euclides ofrece una demostración.

Los Elementos son un compendio de trece libros. Después de la Biblia, es el libro más editado, con más de mil ediciones.

Los Elementos es la obra maestra de Euclides en el campo de la geometría, y ofrece un tratamiento definitivo de la geometría de dos dimensiones (el plano) y tres dimensiones (el espacio), siendo este el origen de lo que ahora conocemos como geometría euclidiana.

Conceptos básicos

Los elementos están conformados por definiciones, nociones comunes y postulados (o axiomas) seguidos de teoremas, construcciones y demostraciones.

– Un punto es aquello que no tiene partes.

– Una línea es una longitud que no tiene anchura.

– Una línea recta es la que yace por igual con relación a los puntos que están en esta.

– Si dos rectas se cortan de forma que los ángulos adyacentes sean iguales, los ángulos se denominan rectos y las líneas se denominan perpendiculares.

– Rectas paralelas son aquellas que, estando en un mismo plano, nunca se cortan.

Luego de estas y otras definiciones, Euclides nos presenta una lista de cinco postulados y cinco nociones.

Nociones comunes

– Dos cosas que son iguales a una tercera, son iguales entre sí.

– Si a cosas iguales se añaden cosas iguales, los resultados son iguales.

– Si a cosas iguales se le restan cosas iguales, los resultados son iguales.

– Las cosas que coinciden entre sí son iguales entre sí.

– El total es mayor que una parte.

Postulados o axiomas

– Por dos puntos distintos pasa una y solo una recta.

– Las líneas rectas pueden extenderse indefinidamente.

– Se puede dibujar un círculo con cualquier centro y cualquier radio.

– Todos los ángulos rectos son iguales.

– Si una línea recta cruza a dos líneas rectas de modo que los ángulos internos de un mismo lado suman menos que dos ángulos rectos, entonces las dos rectas se cruzarán en ese lado.

Este último postulado se conoce como el postulado de las paralelas y fue reformulado de la siguiente manera: “Por un punto exterior a una recta, se puede trazar una única paralela a la recta dada”.

Ejemplos

A continuación, algunos teoremas de los Elementos servirán para mostrar propiedades de espacios geométricos donde se cumplen los cinco postulados de Euclides; además, ilustrarán los razonamientos lógicos-deductivos de los que se valió este matemático.

Primer ejemplo

Proposición 1.4. (LAL)

Si dos triángulos tienen dos lados y el ángulo entre estos iguales, entonces los otros lados y los otros ángulos son iguales.

Demostración

Sean ABC y A’B’C’ dos triángulos con AB=A’B’, AC=A’C’ y los ángulos BAC y B’A’C’ iguales. Desplacemos al triangulo A’B’C’ de modo que A’B’ coincida con AB y que el ángulo B’A’C’ coincida con el ángulo BAC.

Entonces, la línea A’C’ coincide con la línea AC, de modo que C’ coincide con C. Luego, por el postulado 1, la línea BC debe coincidir con la línea B’C’. Por lo tanto los dos triángulos coinciden y, en consecuencia, sus ángulos y sus lados son iguales.

Segundo ejemplo

Proposición 1.5. (Pons Asinorum)

Si un triángulo tiene dos lados iguales, entonces los ángulos opuestos a esos lados son iguales.

Demostración

Supongamos que el triángulo ABC tiene lados AB y AC iguales.

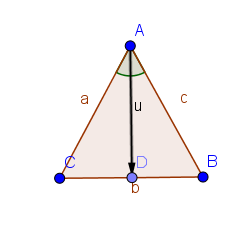
Entonces, los triángulos ABD y ACD tienen dos lados iguales y los ángulos entre estos son iguales. Así, por la proposición 1.4, los ángulos ABD y ACD son iguales.

Tercer ejemplo

Proposición 1.31

Se puede construir una recta paralela a una recta dada por un punto dado.

Construcción

Dada una recta L y un punto P, se traza una recta M que pase por P y corte a L. Luego se traza por P una recta N que corte a L. Ahora, se traza por P una recta N que corte a M, formando un ángulo igual al que L forma con M.

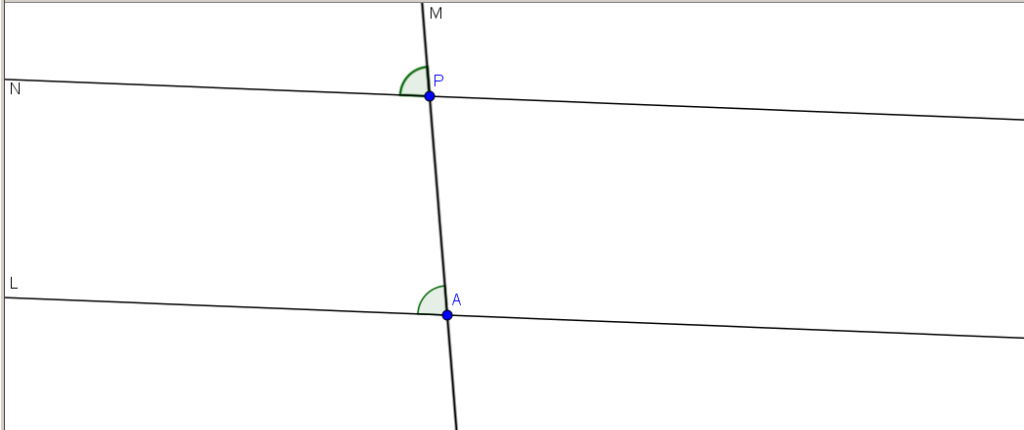
Afirmación

N es paralela a L.

Demostración

Supongamos que L y N no son paralelas y se cortan en un punto A. Sea B un punto en L más allá de A. Consideremos la recta O que pasa por B y P. Entonces, O corta a M formando ángulos que suman menos que dos rectos.

Luego, por 1.5 la recta O debe cortar a la recta L del otro lado de M, así que L y O se cruzan en dos puntos, lo que contradice al postulado 1. Por lo tanto, L y N deben ser paralelas.

Geometría Euclidiana

Fuente: https://ue.aprendiendomas.com.bo/pluginfile.php/400/mod_book/chapter/2224/geometria%20euclidiana.pdf