Imprimir este capítuloImprimir este capítulo

EL LENGUAJE MATEMÁTICO Y LA RELACIÓN CON LAS ACTIVIDADES DE LA VIDA COTIDIANA.

5. Potenciación y radicación de polinomios

Potencia de un polinomio

La potencia de un polinomio, P(x)n, es una forma abreviada de escribir el producto del polinomio n veces:

P ( x ) n = P ( x ) · P ( x ) · ... · P ( x ) ︸ n veces

Calculamos la potencia de un binomio (polinomio de dos términos).

(x + y)1 = x + y

(x + y)2 = (x + y) · (x + y) = x2 + 2xy + y2

(x + y)3 = (x + y) · (x + y)2 = x3 + 3x2y + 3xy2 + y3

Para apreciar las regularidades entre los coeficientes de las distintas potencias ordenamos los resultados.

Potencia

Resultado

Coeficientes

(a + b)1

a + b

1 1

(a + b)2

a2 + 2ab + b2

1 2 1

(a + b)3

a3 + 3a2b + 3ab2 + b3

1 3 3 1

(a + b)4

a4 + 4a3b + 6a2b2 + 4ab3 + b4

1 4 6 4 1

Nos fijamos en la regla que siguen los coeficientes de (a + b)4:

(a + b)4 = 1 · a4-0 · b0 + 4 · a4-1 · b1 + 6 · a4-2 · b2 + 4 · a4-3 · b3 + 1 · a4-4 · b4 = a4 + 4a3b + 6a2b2 + 4ab3 + b4

La relación existente entre los coeficientes de las distintas potencias de un binomio se conoce con el nombre de triángulo de Tartaglia.

Todas las filas comienzan y acaban con un 1, y los demás coeficientes se obtienen sumando los términos contiguos de la fila anterior.

Raíz cuadrada de un polinomio.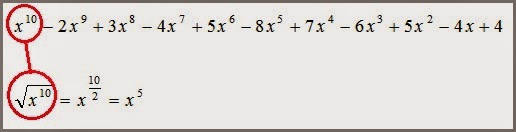
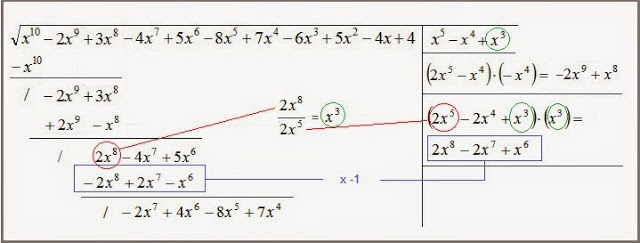
Para hallar la raíz cuadrada de un polinomio se seguirán una serie de pasos que pasamos a describir con un ejemplo para su mayor entendimiento.

Vamos a hallar la raíz cuadrada del siguiente polinomio:



1) Lo primero de todo es comprobar que el polinomio esté ordenado. En este caso está ordenado con respecto a la "x" de forma descendente, por lo que ya podemos empezar a operar para extraer la raíz.

  2) El siguiente paso es hallar la raíz cuadrada de su primer término.



El resultado será el primer término de la raíz cuadrada.

Seguidamente elevamos al cuadrado esta raíz y se resta al polinomio.



 3) El próximo paso es bajar los dos siguientes términos del polinomio y dividimos el primero por el doble del primer término de la raíz. El resultado obtenido es el segundo miembro de la raíz.


untamos el doble del primer término con el nuevo término obtenido y formamos un binomio. Multiplicamos este binomio por el nuevo término obtenido y el resultado se resta de los dos términos que habíamos bajado. Seguidamente bajamos los dos siguientes términos para tener un trinomio.


4) Se divide el primer término del residuo por el doble del primer término de la raíz ya hallada hasta ahora. El resultado es el tercer término de la raíz. Formamos un trinomio con el doble de la raíz ya hallada y este tercer término y lo multiplicamos por dicho tercer término. El resultado se resta del residuo.


5) Se sigue el mismo procedimiento teniendo en cuenta que:

  • A cada residuo obtenido se le añadirán tantos términos del polinomio subradical como sean necesarios para que el residuo resultante tenga un término más que el residuo de la operación anterior.
  • Hemos de dividir siempre el primer término del residuo que se obtenga entre el doble del primer término de la raíz obtenida hasta el momento, que siempre claro está será el mismo. El cociente obtenido será siempre el siguiente término de la raíz.
  • Crearemos siempre un polinomio con el doble de la raíz obtenida hasta el momento y el cociente obtenido del apartado anterior que al multiplicarlo por dicho cociente nos dará como resultado otro polinomio que se restará al residuo.

Terminamos de calcular la raíz.