EL LENGUAJE MATEMÁTICO Y LA RELACIÓN CON LAS ACTIVIDADES DE LA VIDA COTIDIANA.
4. La regla de Ruffini y el teorema del resto.
Con la regla de Ruffini, solamente se obtienen las soluciones enteras. Si la ecuación tiene soluciones complejas o reales, éste método no es válido.
Veremos que para obtener las soluciones de la ecuación, previamente hay que factorizar, por lo que con el mismo ejemplo explicaremos ambos conceptos.
Vamos a resolver un ejemplo explicando paso por paso.
Tenemos la siguiente ecuación:
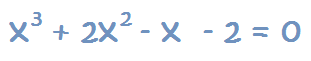
1 – Identificamos los coeficientes de cada término, que son los números que van delante de la incógnita. Para la ecuación anterior, los represento en verde para identificarlos:
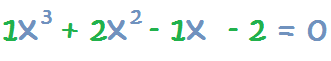
2 – Trazamos dos líneas perpendiculares de esta forma:

3 – Colocamos los coeficientes ordenados por su grado de mayor o menor:
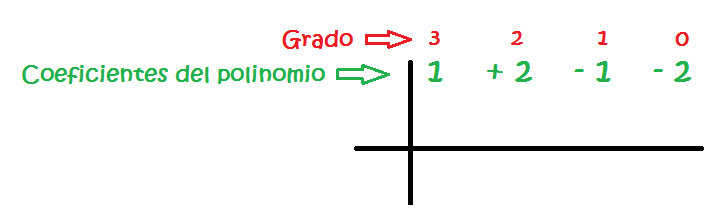
En la regla de Ruffini, el grado va disminuyendo de 1 en 1 y cada grado tiene su lugar. Por ejemplo si no tuviérmos ningún término que tenga x², en el lugar del grado 2, se colocaría un 0.
Los números que hemos escrito hasta ahora en el método de Ruffini, es equivalente a escribir la ecuación, es decir:

4 – Ahora escribimos un número a la izquierda de la línea vertical. Más adelante explicaremos qué número colocar aquí y por qué. De momento, empezamos con el 1.
Ese número corresponde al número (a) del binomio x – a:
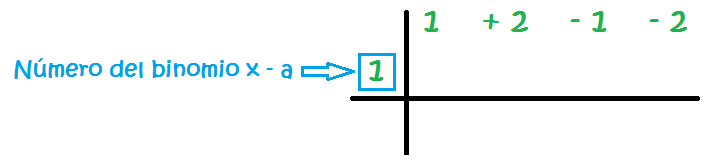
En este caso, escribir ahí un 1, significa el binomio (x – 1) en el método de Ruffini

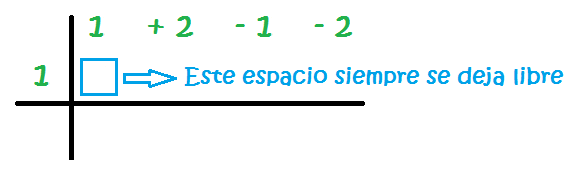
6 – Se hace la suma de la primera columna y el resultado de pone abajo:
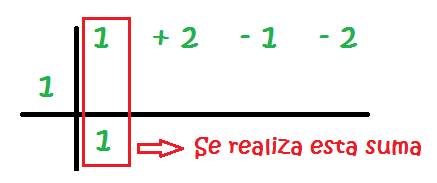
7 – Se multiplica el número de la izquierda por el resultado de la suma de la primera columna. El resultado se coloca en el hueco de la segunda columna:

8 – Se realiza la suma de la segunda columna:
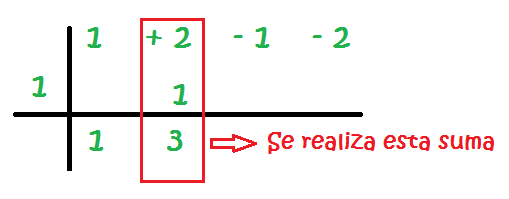
9 – Se multiplica el número de la izquierda por el resultado de la suma de la segunda columna. El resultado se coloca en el hueco de la tercera columna:
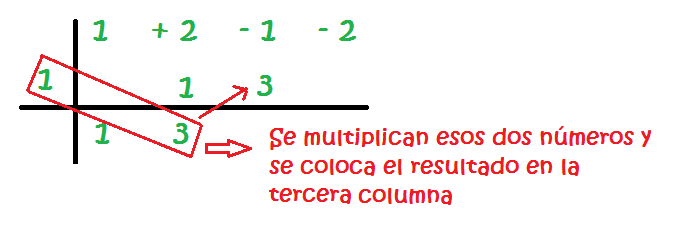
10 – Así sucesivamente hasta completar todas las columnas:
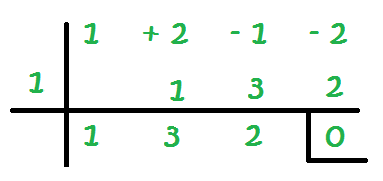
El objetivo es que en la última columna tengamos un 0. Esta es la explicación de qué número colocar a la izquierda de la línea:
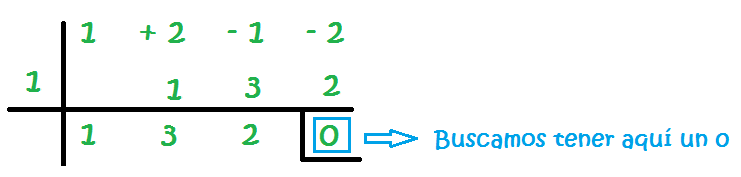
Si no tenemos un cero, tendríamos que probar con otro número a la izquierda de la línea vertical y reiniciar el proceso.
En el Curso de Polinomios, te enseño el método para que encuentres con facilidad el número para que resulte 0 en la última columna. Además de aprender como hacer Ruffini, tendrás más ejemplos del método de Ruffini y ejercicios explicados paso a paso.
Una vez hemos obtenido un cero al final, vamos a ver qué significa lo que tenemos hasta aquí:
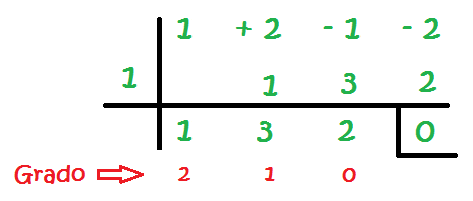
Lo que nos ha quedado en la última fila es otra ecuación, pero ahora, el número que está a la izquierda del 0, tiene grado 0 y éste va aumentando de 1 en 1 hacia la izquierda. En este caso, nos queda lo equivalente a tener esta ecuación:

Y como hemos visto antes, el 1 a la izquierda de la línea vertical significaba:

Lo que quiere decir que lo que tenemos hasta ahora es el producto de esas dos ecuaciones, que es igual a la ecuación original:
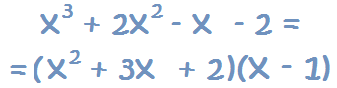
11 – Con la fila que nos ha quedado, volvemos a empezar. Empezamos probando con el 1:
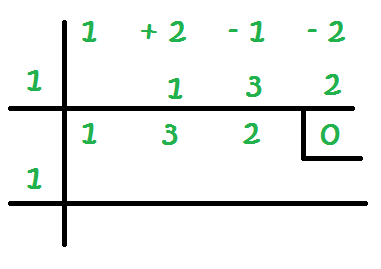
12 – Igual que antes, vamos multiplicando con el resultado de sumar en cada columna:
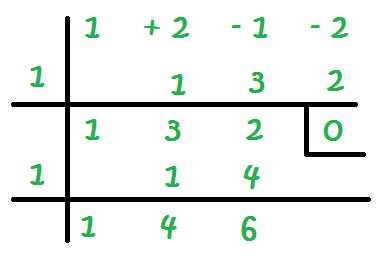
Al final tenemos un 6, y lo que queremos es tener un cero. Por tanto, debemos seguir probando, con -1, con 2, con -2… hasta encontrar el número que nos haga tener un cero en la última columna.
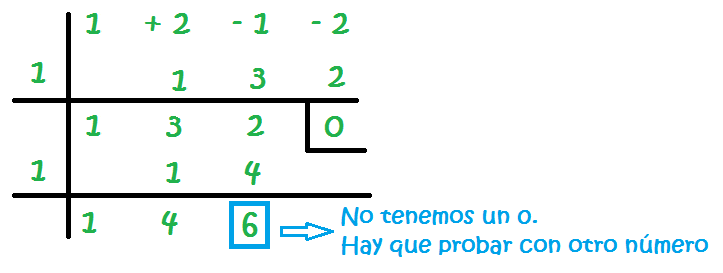
El número que nos hace tener un 0 al final es el -2:
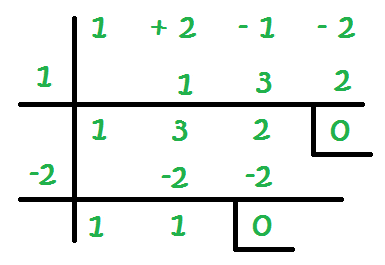
¿Y ahora que hacemos? ¿Cómo sabemos que hemos terminado?
El mayor grado de la última fila es 1, por tanto hemos terminado:
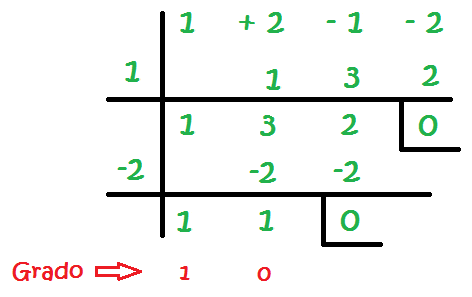
El resultado de la factorización de la ecuacuón por el método de Ruffini es el producto de la última fila y de los números que están a la izquierda de la línea vertical, pero expresados en forma de ecuación:

![]()
![]()
Por tanto, nuestra ecuación será:
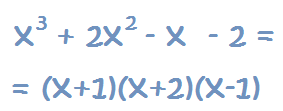
Hasta aquí hemos factorizado la ecuación. Ahora vamos a resolverla: 1 – Igualamos a 0, tal y como estaba en un principio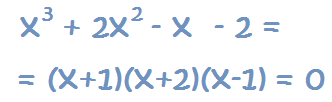
2 – Recuerda que cuando una multiplicación de dos o más factores tiene como resultado 0, quiere decir que uno de los factores es 0, ya que cualquier valor multiplicado por 0 es 0. Por tanto, cualquier factor podría ser 0.
Nos quedan tres ecuaciones de primer grado para despejar, de donde obtenemos las tres soluciones (ya que es una ecuación de tercer grado):
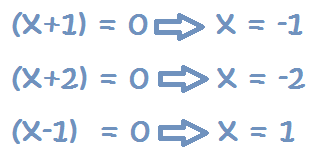
Soluciones: -1, -2 y 1