EL NÚMERO, LA FORMA Y EL CÁLCULO EN LA SOLUCIÓN DE PROBLEMAS O SITUACIONES DE CONTEXTO.
3. Los números reales (ℝ) y su Relación de orden.
3.2. Operaciones en (ℝ): Potenciación, radicación y sus propiedades.
Potenciación
Multiplicar un número b por sí mismo varias veces, puede indicarse como bn ,
que es lo mismo que multiplicar b, n veces: bn = b.b.b ....b
El número b se llama “base” y el n se llama “exponente” y decimos que bn es la
n-esima potencia de b.
Reglas de los exponentes
Producto de potencias de igual base
Para multiplicar dos o más potencias que tienen la misma base basta con sumar los exponentes y aplicarlo a la base; bm . bn = b(m+n)
Producto de cocientes de igual base
Para dividir dos o más potencias que tienen la misma base basta con restar los exponentes y aplicarlo a la base; bm/ bn = bn-m si b es distinto de cero
Potencia de Potencia
Para resolver la potencia de una potencia se multiplican los exponentes y se aplican a la base (bn)m=bn.m
Ley distributiva respecto del producto (a.b)n=an.bn
Ley distributiva respecto del cociente (a/b)n=a/bn si b es distinto de cero
Potencia cero: Por convención b0= 1 ¿A qué será igual 00 ? ¿Existe?
Exponente Negativo: (b)-n=1/bn
Leyes de los signos
Si la base es positiva el resultado es positivo cualquiera sea el exponente
b3=b.b.b
b4=b.b.b.b
Si la base es negativa, el resultado es negativo si el exponente es impar
(-b)3=(-b).(-b).(-b)=-b3
Si la base es negativa, el resultado es positivo si el exponente es par 4
(-b)4=(-b).(-b).(-b).(-b)=-b4
Radicación
La operación de radicación es la inversa de la potenciación, si an = b entonces diremos que n√b= a, donde b es el radicando, n es el índice de la raíz y a es raíz de b.
٠ la raíz es positiva si b es positivo
٠ es negativa si b es negativo y n es impar
Leyes de la radicación
Distributiva respecto del producto y respecto del cociente
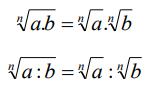
Potencia de una raíz
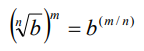
Esto implica que todo índice de una radicación puede escribirse como una potencia de
exponente fraccionario